はじめに

こんにちは、データサイエンティストの森下です。本記事では所謂ブラックボックスモデルを解釈する方法を紹介したいと思います。

RF/GBDT/NNなどの機械学習モデルは古典的な線形回帰モデルよりも高い予測精度が得られる一方で、インプットとアウトプットの関係がよくわからないという解釈性の問題を抱えています。この予測精度と解釈性のトレードオフでどちらに重点を置くかは解くべきタスクによって変わってくると思いますが、たとえばTVISIONでのデータ分析はクライアントの意思決定に繋げる必要があり、解釈性に重きを置いていることが多いです。

とはいえ機械学習モデルの高い予測精度は惜しく、悩ましかったのですが、学習アルゴリズムによらずモデルに解釈性を与えられる手法が注目され始めました。そこで、本記事では変数重要度とPDP/ICE Plot (Partial Dependence/Individual Conditional Expectation)を用いて所謂ブラックボックスモデルを解釈する方法を紹介します。

モデルの学習

まずはパッケージを読み込みます。

library(tidyverse)
library(tidymodels)

library(pdp) # partial dependence plot
library(vip) # variable importance plot

例によってdiamondsデータを使用し、Rondom Forestでダイヤの価格を予測するモデルを作ります。 tidymodelsの使い方は記事をご覧下さい。

set.seed(42)

df_split = initial_split(diamonds,  p = 0.9)

df_train = training(df_split)
df_test  = testing(df_split)


rec = recipe(price ~ carat + clarity + color + cut, data = df_train) %>% 
  step_log(price) %>% 
  step_ordinalscore(all_nominal()) %>% 
  prep(df_train)

df_train_baked = juice(rec)
df_test_baked = bake(rec, df_test)

fitted = rand_forest(mode = "regression", 
                     trees = 100,
                     min_n = 5,
                     mtry = 2) %>% 
  set_engine("ranger", num.threads = parallel::detectCores(), seed = 42) %>% 
  fit(price ~ ., data = juice(rec))

> fitted
parsnip model object

Ranger result

Call:
 ranger::ranger(formula = formula, data = data, mtry = ~2, num.trees = ~100,      min.node.size = ~5, num.threads = ~parallel::detectCores(),      seed = ~42, verbose = FALSE) 

Type:                             Regression 
Number of trees:                  100 
Sample size:                      48547 
Number of independent variables:  4 
Mtry:                             2 
Target node size:                 5 
Variable importance mode:         none 
Splitrule:                        variance 
OOB prediction error (MSE):       0.01084834 
R squared (OOB):                  0.9894755

変数重要度

モデルの解釈において最も重要なのは、どの変数がアウトプットに強く影響し、どの変数は影響しないのかを特定すること、つまり変数重要度を見ることだと思います。たとえば特に重要な変数を見定めて施策を打つことでアウトプットをより効率よく改善できる可能性が高まりますし*1、ありえない変数の重要度が高く出ていればデータやモデルが間違っていることに気づけるかもしれません。

tree系のアルゴリズムだとSplit（分割の回数）やGain（分割したときの誤差の減少量）などで変数重要度を定義することもできますが、ここではアルゴリズムに依存しない変数重要度であるPermutationベースのものを紹介します。 Permutationベースの変数重要度のコンセプトは極めて直感的で、「ある変数の情報を壊した時にモデルの予測精度がすごく落ちるならそれは大事な変数だ」というものです。

f:id:dropout009:20190107002315p:plain

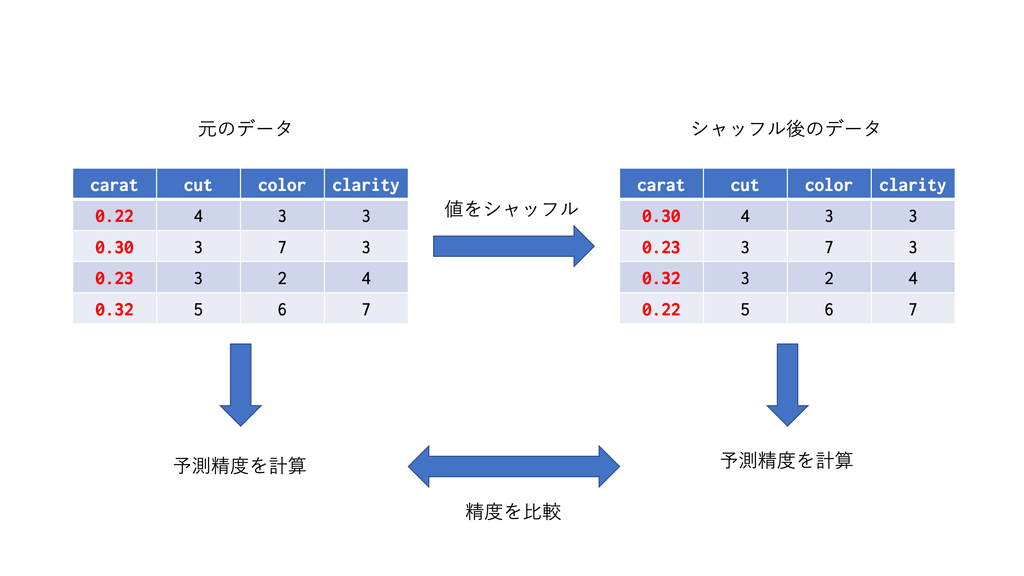
たとえば今回のモデルでcaratの変数重要度を見たいとします。

訓練データを使って学習済みモデルを用意し、テストデータに対する予測精度を出します。
テストデータのcarat列の値をシャッフルしますし、シャッフル済みテストデータを使って同様に予測を行います。
2つの予測精度を比較し、予測精度の減少度合いを変数重要度とします。

carat列のシャッフルによって、もしcaratが重要な変数ならモデルは的はずれな予測をするようになりますし、逆に重要でないなら特に影響は出ないはずで、これはある意味においての変数の重要度を捉えらていると思います。

また、この手法はあくまで予測の際に用いるデータをシャッフルしていて、学習をやり直しているわけではないため、計算が軽いことも利点です。

さて、実際にPermutationベースの変数重要度を計算してみましょう。パッケージはvipを使います。変数重要度が計算できるパッケージは他にもいくつかありますが、vipはPermutationベースの変数重要度が計算でき、次に見るPartial Dependence Plotで利用するパッケージpdpと同じシンタックスが使えます（作者が同じなので）

# objectとnewdataを受けて予測結果をベクトルで返す関数を作っておく必要がある
pred_wrapper = function(object, newdata) {
  return(predict(object, newdata) %>% pull(.pred))
}


fitted %>% 
  vip(method = "permute",  # 変数重要度の計算方法
      pred_fun = pred_wrapper, 
      target = df_test_baked %>% pull(price),
      train = df_test_baked %>% select(-price),
      metric = "rsquared", # 予測精度の評価関数)

f:id:dropout009:20190106230934p:plain

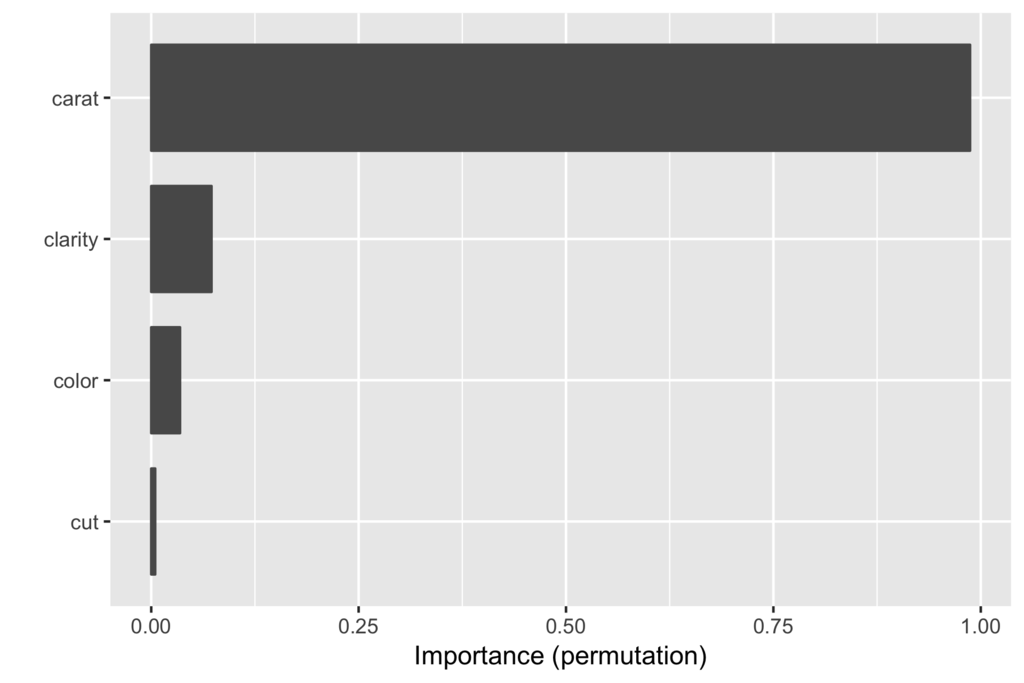
一番手っ取り早い方法はvip()関数を使った可視化です（グラフを自分で細かくいじりたい場合はvi()での計算結果を自分で可視化します）。 caratの変数重要度がその他の変数と比べてダントツであることが見て取れます。

Partial Dependence Plot

各変数の重要度がわかったら、次に行うべきは重要な変数とアウトカムの関係を見ることだと思います。ただ、一般にブラックボックスモデルにおいてインプットとアウトカムの関係は非常に複雑で、可視化することは困難です。

そこで、複雑な関係を要約する手法の一つにPartial Dependence Plot(PDP)があります。PDPは興味のある変数以外の影響を周辺化して消してしまうことで、インプットとアウトカムの関係を単純化しようというものです。

特徴量を $x$ とした学習済みモデル $\hat{f}(x)$ があるとします。 $x$ を興味のある変数 $x_s$ とその他の変数 $x_c$ に分割し、以下のpartial dependence function

\begin{align} \hat{f_{s}}(x_s) = E_c\left[ \hat{f}(x_s, x_c) \right] = \int \hat{f}(x_s, x_c) p(x_c) d x_c \end{align}

を定義し、これを

\begin{align} \bar{f_{s}}(x_s) = \frac{1}{N}\sum_i\hat{f}\left(x_s, x_c^{(i)}\right) \end{align}

で推定します。具体的には以下のようなことをやっています。

f:id:dropout009:20190107002309p:plain

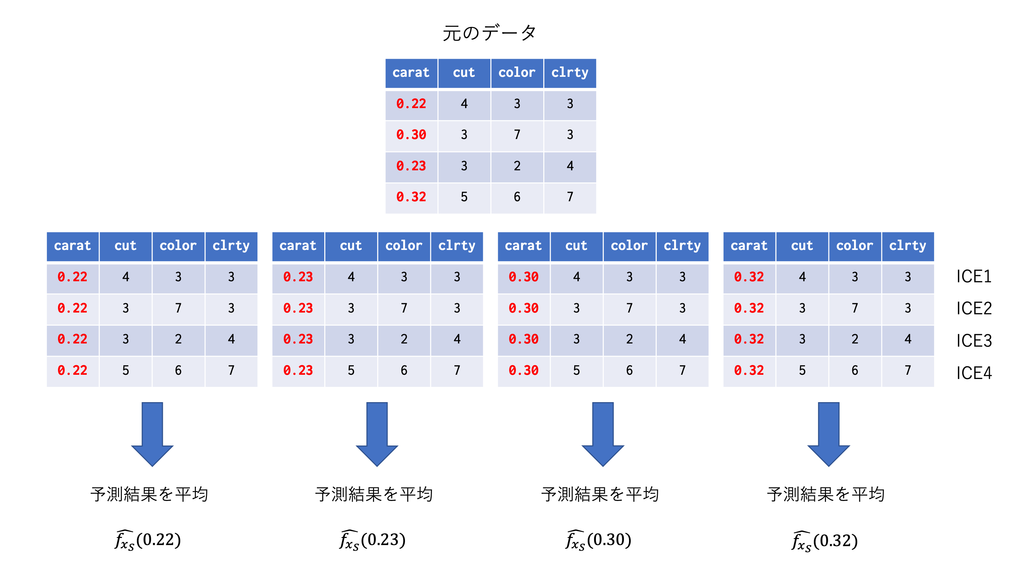
なお、PDPは平均をとりますが、平均を取らずに各 $i$ について個別にプロットしたものをIndividual Conditional Expectation (ICE) Plotと呼びます。インプットとアウトカムの関係が各 $i$ によって違う場合に有効となります。

それでは、特に重要だった変数caratについて実際にPDPを作成してみましょう。パッケージはpdpを使います。

ice_carat = fitted %>% 
  partial(pred.var = "carat",
          pred.fun = pred_wrapper,
          train = df_test_baked, 
          type = "regression")

ice_carat %>% 
  autoplot()

f:id:dropout009:20190107011226p:plain

partial()でPD/ICE Plotの元となるデータを計算できます。細部にこだわらなければautoplot()で可視化するのが一番手っ取り早いです。赤い線がPDP、黒い線がICEになります。caratがlog(price)に与える影響が徐々に逓減していく様子が見て取れます。特徴量に明示的な変換を施さなくても非線形の関係を捉えることができるのがRF+PDPの強力な点かと思います。

まとめ

モデルの解釈性は意思決定に繋がるデータ分析として重要
変数重要度とPDPでアルゴリズムによらずブラックボックスモデルを解釈することができる

アルゴリズムによらずモデルを解釈する手法としては他にもALE、SHAP value、LIMEなどがあり、次回以降に紹介できればと思っています。

参考

*1:変数間の関係が相関関係なのか因果関係なのかという問題はありますが

REVISIO Tech Blog

変数重要度とPartial Dependence Plotでブラックボックスモデルを解釈する

はじめに

モデルの学習

変数重要度

Partial Dependence Plot

まとめ

参考